Depuis quelques jours CovidTracker prend de l’ampleur, vous avez été plus de 30 000 à l’avoir consulté et je souhaite vous remercier chaleureusement. Ces derniers jours, il a notamment été relayé par France 3 Lorraine, TELECOM Nancy et l’Université de Lorraine. C’est par ce biais que Philippe Brouard (Université de Lorraine) l’a découvert.

Philippe a développé un modèle empirique de l’épidémie de Coronavirus en France. Il m’a proposé de travailler ensemble afin de continuer à améliorer ce modèle, et de le partager au plus grand nombre. Vous trouverez ci-dessous un article décrivant le fonctionnement du modèle. Nous publierons ensuite dans quelques jours des prédictions sur l’évolution du virus en France, d’après son modèle, dans un contexte de déconfinement. Bonne lecture !

— Guillaume

Article de Philippe Brouard :

Pourquoi voit-on une baisse du nombre d’hospitalisations pendant une augmentation des cas covid-19 ?

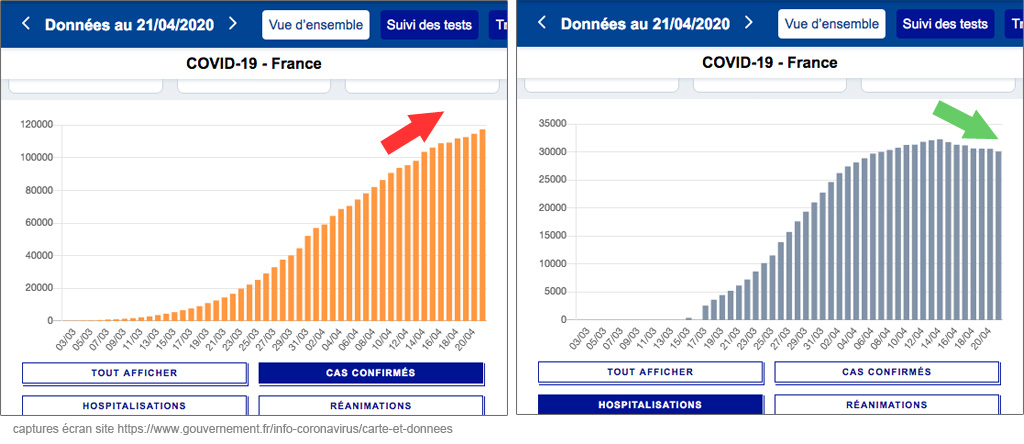
Grâce aux données numériques publiées par Santé publique France (merci pour cet effort de transparence) et aux analyses réalisées sur COVIDTRACKER, nous avons accès à l’évolution de l’épidémie de covid-19 en France. Un constat m’a interpellé : le nombre de cas confirmés ne cesse de croître depuis le 3 mars 2020, pourtant le nombre d’hospitalisations baisse depuis le 14 avril 2020. Comment expliquer cette situation qui peut paraître contradictoire ?

Recherche d’un scénario de patient covid-19

En me penchant sur cette question initiale, j’ai recherché à modéliser le circuit du patient à l’hôpital. Voici une proposition de schéma :

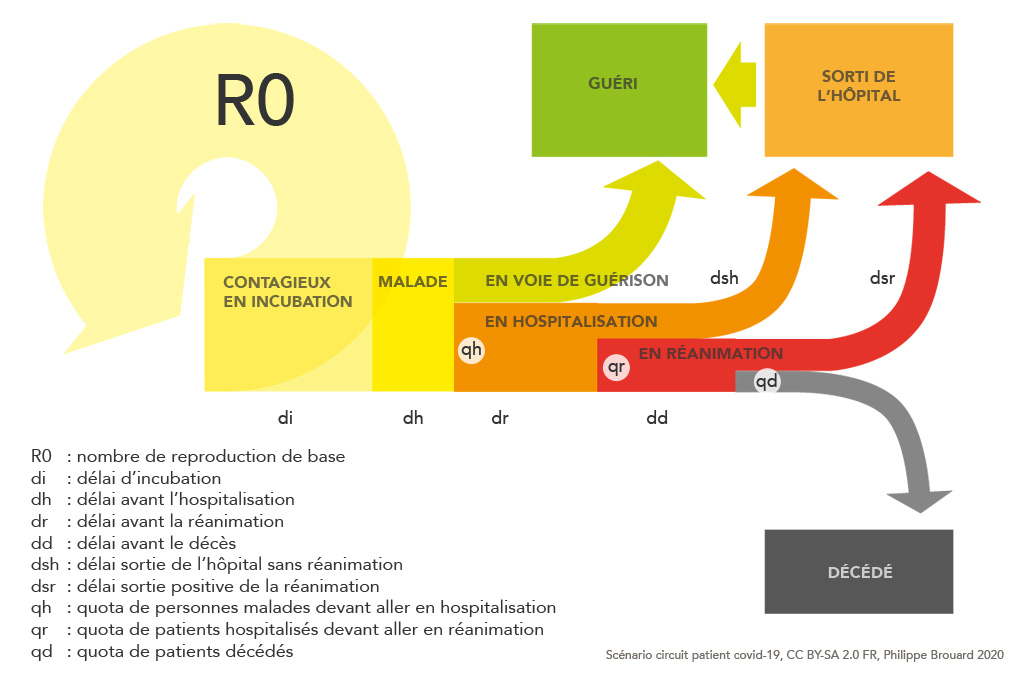
La combinaison de plusieurs variables de délai, de quota de passage, et de nombre de reproduction de base pourrait expliquer l’effet retard entre l’accroissement des cas positifs de covid-19 et plus tard une baisse des hospitalisations.

Le schéma présente le fameux nombre R0, essentiel dans l’évolution d’une épidémie. Il peut se définir comme le nombre de personnes qui seront contaminées par l’intermédiaire d’une personne contagieuse pendant la durée de sa contagiosité. Si R0 = 1, toute personne contagieuse en contamine une autre et donc le phénomène tourne en boucle longtemps : l’épidémie continue à se propager sur la population. Si R0 est inférieur à 1, petit à petit l’épidémie ralentit. Si R0 est supérieur à 1, l’épidémie s’emballe et c’est le scénario de la croissance exponentielle qui se met en marche.

Pendant la croissance du nombre de cas positifs covid-19, au bout d’un certain délai, des patients sortent de l’hôpital, soit en étant en meilleur santé, soit malheureusement en étant décédés. Ils libèrent ainsi des places pour des nouveaux patients. La différence entre les entrées et les sorties de l’hôpital a pour conséquence l’évolution du nombre d’hospitalisations. Est-ce que cette variation converge vers une certaine valeur ? C’est l’objectif d’une vérification par modèle mathématique.

Recherche d’un algorithme de calcul du nombre d’hospitalisations

Pour commencer avec un premier modèle numérique, l’objectif est de reproduire la courbe des hospitalisations en s’appuyant sur les données de Santé publique France : nombre de cas positifs. Pour faire le code informatique, il faut utiliser les variables du schéma scénario présenté en début d’article. Voici ma proposition d’algorithme de calcul. C’est compliqué, alors si vous n’êtes pas passionné de programmation vous pouvez passer à la suite de l’article.

Les délais varient en jours.
Les quotas varient entre 0 et 1.

Nombre d'hospitalisations du jour
= Nombre d'hospitalisations de la veille
+ Nombre d'entrées du jour à l'hôpital
- Nombre de sorties du jour de personnes en voie de guérison
- Nombre de sorties du jour de personnes quittant la réanimation
- Nombre de décès du jour

Étant préalablement calculé que 

Nombre d'entrées du jour à l'hôpital
= Nombre de nouveaux cas positifs au jour précédent le délai avant hospitalisation (dh)
* quota de personnes malades devant aller à l'hôpital (qh)

Nombre de sorties du jour de personnes en voie de guérison
= Nombre de personnes entrées à l'hôpital au jour précédent le délai avant sortie en voie de guérison (dsh)
* quota de personnes hospitalisées qui guérissent sans passer par la réanimation (1-qr)

Nombre de sorties du jour de personnes quittant la réanimation
= Nombre de personnes entrées en réanimation au jour précédent le délai avant sortie positive de la réanimation (dsr)
* quota de personnes qui sortent de réanimation en voie de guérison (1-qd)

Nombre de décès du jour
= Nombre de personnes entrées en réanimation au jour précédent le délai avant décès en réanimation (dd)
* quota de personnes qui décèdent en réanimation (qd)

Étant préalablement calculé que

Nombre de personnes qui entrent en réanimation à une date donnée
= Nombre de personnes entrées à l'hôpital au jour précédent le délai avant passage en réanimation (dr)
* quota de personnes hospitalisées qui entrent en réanimation (qr)

Étant préalablement calculé que

Nombre de nouveaux cas positifs
= nombre cumulé de cas positifs du jour
- nombre cumulé de cas positifs de la veille

Si les lecteurs suivent toujours, félicitations à vous.

Le fonctionnement de propagation de l’épidémie semble être récursif, ce qui fait penser aux suites mathématiques. En quelques sortes on fait régulièrement appel à une valeur passée pour calculer une valeur en cours. Un tableur est un outil pratique pour construire ce modèle. Après mes nombreux tâtonnements, une première version du calculateur a donné le graphique suivant. En jaune et en orange, les valeurs de Santé publique France. En couleur mandarine, les valeurs du calculateur.

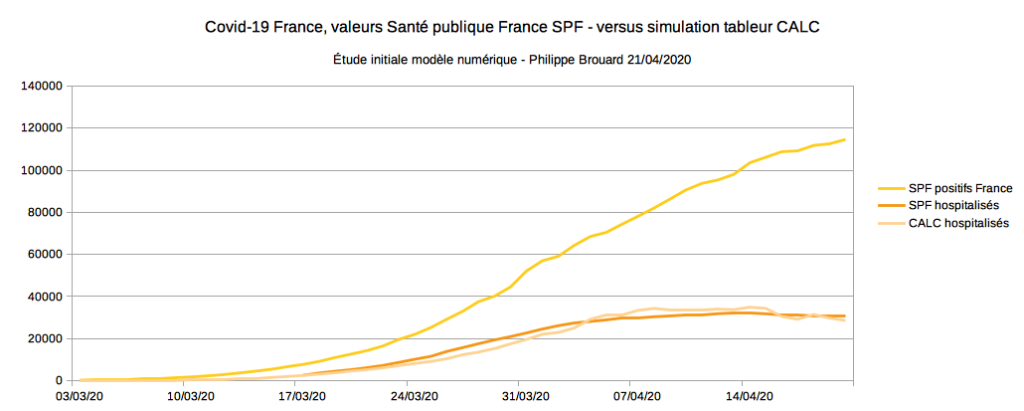
Pour ajuster le profil de la courbe couleur mandarine sur la courbe couleur orange (car elles doivent représenter la même réalité), j’ai procédé par essais et corrections successives. J’ai commencé par m’inspirer des informations communiquées par voie de presse. Par exemple le délai entre le moment où une personne est attestée positive et le moment où elle doit aller à l’hôpital en cas de complication : peut-être environ 4 jours ? Si la situation du patient se dégrade sérieusement à l’hôpital, le scénario conduit à un passage en réanimation au bout de… peut-être environ 3 jours ? Et ainsi de suite. Si la courbe calculée s’écarte de la référence, il faut corriger une des valeurs dans un sens ou dans un autre. Les réglages du modèle numérique obtenus à ce moment là sont approximatifs. Pour autant l’algorithme semble bien reproduire le cas à modéliser : le nombre d’hospitalisations commence à baisser même si le nombre de cas positifs augmente.

Perfectionnement du modèle numérique avec la modélisation de la courbe des cas positifs

À la suite de ce premier modèle, j’ai pensé que la modélisation de la courbe des cas de tests positifs pouvait être la suite logique du travail de programmation. Il s’agit de traduire en algorithme la boucle R0 qui démarre le scénario. À nouveau, si vous n’êtes pas passionné d’informatique, vous pouvez passer à la suite de l’article.

Délai exprimé en jours

Nombre de cas positifs du jour
= Nombre de cas positifs de la veille
+ 
(Nombre de nouveaux cas positifs au jour précédent le délai de la période contagieuse
* Nombre de reproduction de base R0)

Étant préalablement calculé 

Nombre de nouveaux cas positifs à une date donnée
= Nombre de cas positifs à cette date
- Nombre de cas positifs de la veille

Cette algorithme en boucle fonctionne s’il y a un petit échantillon initial de cas positifs à une date reculée dans le temps qui amorce la propagation. J’ai choisi de prendre comme déclencheur l’effectif du groupe de cas positif anciens, historisé dans les données du tableau mondial de l’épidémie. Je retiens la date avant l’accroissement de la courbe des cas positifs : un groupe de 12 personnes le 15 février 2020.

Le programme en boucle donne des résultats très variables selon la valeur de R0. Ce R0 est un reflet de la situation épidémiologique comme indiqué au début de l’article. Pour rappel, s’il est inférieur à 1, le nombre de cas positifs a tendance à décélérer et s’il est supérieur à 1, le nombre de cas positifs a tendance à accélérer.

Dans l’intervalle de temps qui sépare le 15 février à aujourd’hui, les conditions épidémiologiques ont varié. Donc j’ai choisi d’entraîner l’algorithme de calcul avec une temporalité de trois périodes :

• Période A du 15 février au 15 mars, le virus circule librement, la boucle fonctionne avec une valeur RA.
• Période B du 16 mars au 22 mars, mise en place express du confinement partiel de la population française, la boucle fonctionne avec une valeur RB.
• Période C du 23 mars au 10 mai, la situation actuelle où une très grande partie de la population française est confinée, la boucle fonctionne avec une valeur RC.

Nouveaux calculs du modèle numérique

À la suite de nouveaux tâtonnements, essais et corrections sur les variables, j’ai pu obtenir le graphique suivant qui reflète l’évolution de l’épidémie sur une période plus grande. En couleurs foncées, les valeurs de Santé publique France. En couleurs claires, les valeurs calculées par l’algorithme.

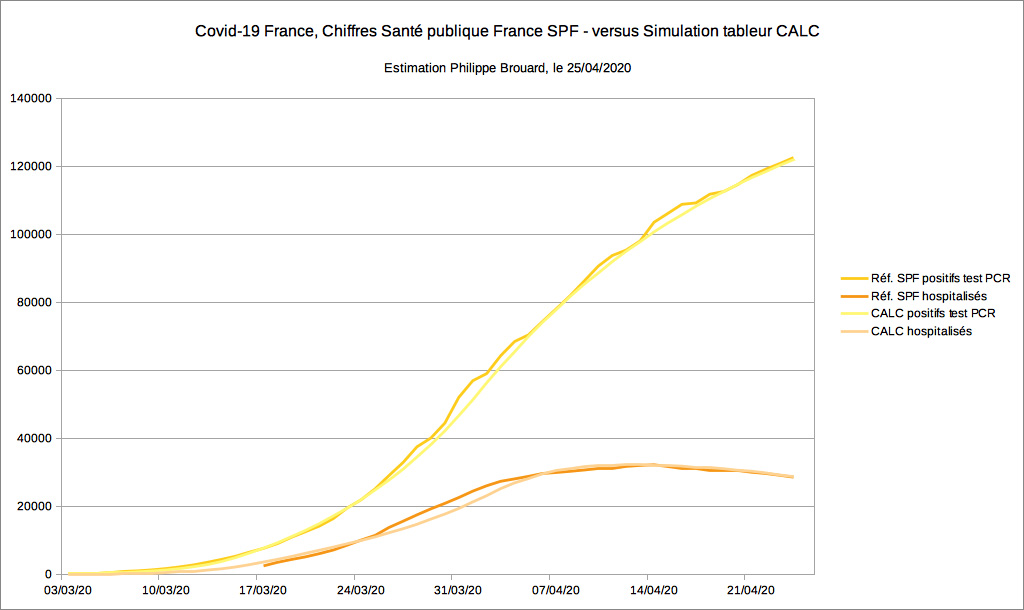
Le modèle mathématique se révèle plus performant : il donne un résultat qui « colle » plutôt bien à la réalité. Pour ainsi dire, les courbes de même couleur sont proches. Les valeurs calculées par le simulateur ne sont pas trop éloignées des valeurs de référence. Le fait d’avoir un effet « lissé » sur la courbe jaune clair des tests positifs calculés a comme conséquence directe de lisser aussi la courbe couleur mandarine.

Mon analyse

Ce graphique prospectif conforte la possibilité de construire un modèle numérique de l’évolution de l’épidémie covid-19 en France. Le travail va continuer sur le site COVIDTRACKER en commun avec Guillaume Rozier.

Restez connectés pour être informés de la suite. Les prochains jours seront l’occasion de mettre à l’épreuve ce simulateur. Nous publierons très prochainement des prédictions sur l’évolution du virus en France basées sur le modèle.

En attendant, #RestezChezVous, prenez soin de vous et de vos proches.

---

Philippe Brouard

Ingénieur en informatique à l’Université de Lorraine